データを整理する
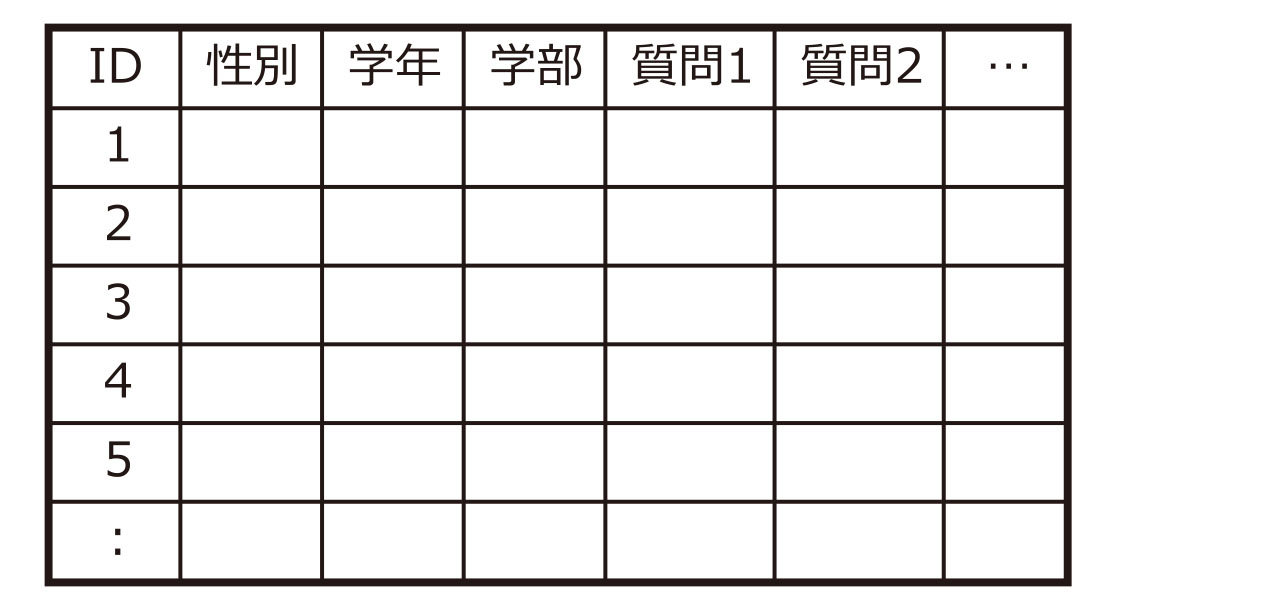
質問紙で集めたデータは「Excel」などの表計算ソフトに入力して、分析しやすい形に整理します。これを「データセットを作る」と呼びます。標準的なデータセットの作り方は次の通りです。
- 質問紙にID番号を振り、ID番号順に入力します。データセットでは、1列目をID番号とし、上から下に向かって1番から順に入力します。2列目以降に、質問紙で得た属性や調査結果を入力します。
- 属性のデータは、コード化します。例えば、「男性=1、女性=2」「自宅生=1、下宿生=2」として、入力します。
- 質問紙で回答されていない項目は、欠損値として扱います。空欄のままにするか、欠損値を表すコード(99など)を入力します。
- データセットが完成したら、入力したデータを確認します。入力ミスがあると分析結果が信頼できなくなります。質問紙とデータセットをつきあわせながら、入力ミスがないかを確認します。可能であれば、入力者とは別の人が確認するとよいでしょう。
- データセットのバックアップを取ります。リムーバブルメディアやクラウドストレージなど、複数の場所にデータをコピーしておくと、作業中にデータが壊れた際に容易にリカバリーすることができます。
比較で属性や行動・経験間の違いを確認する
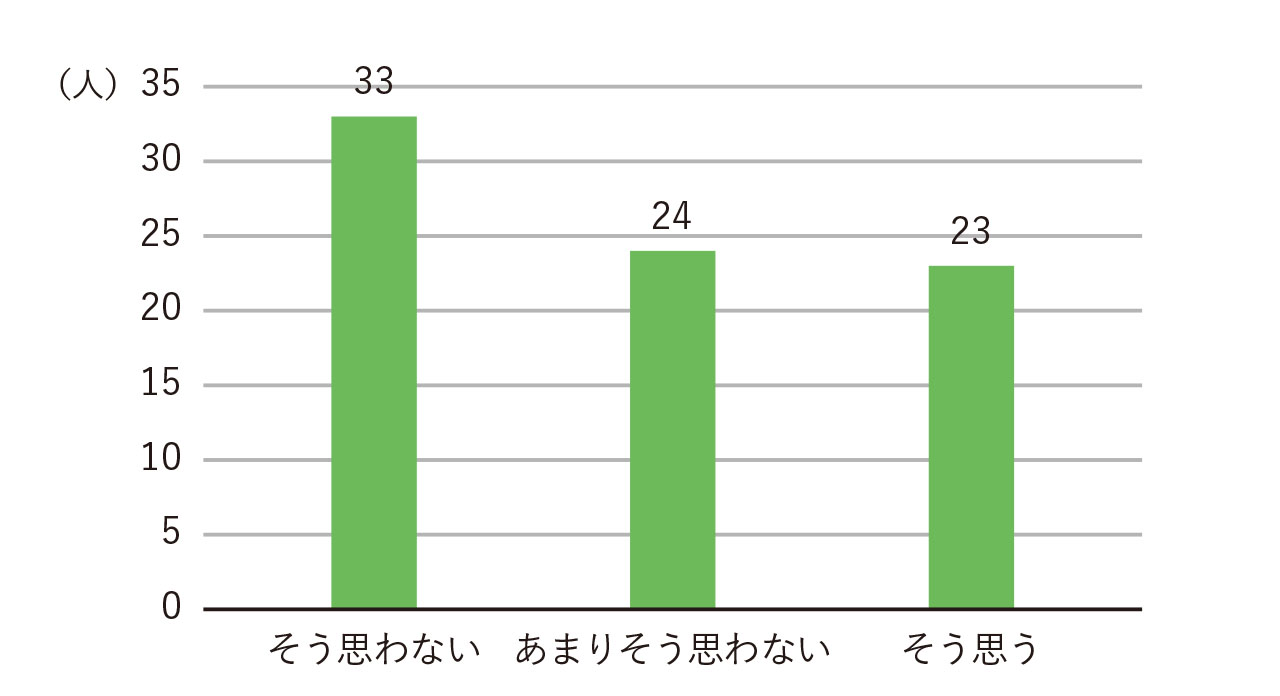
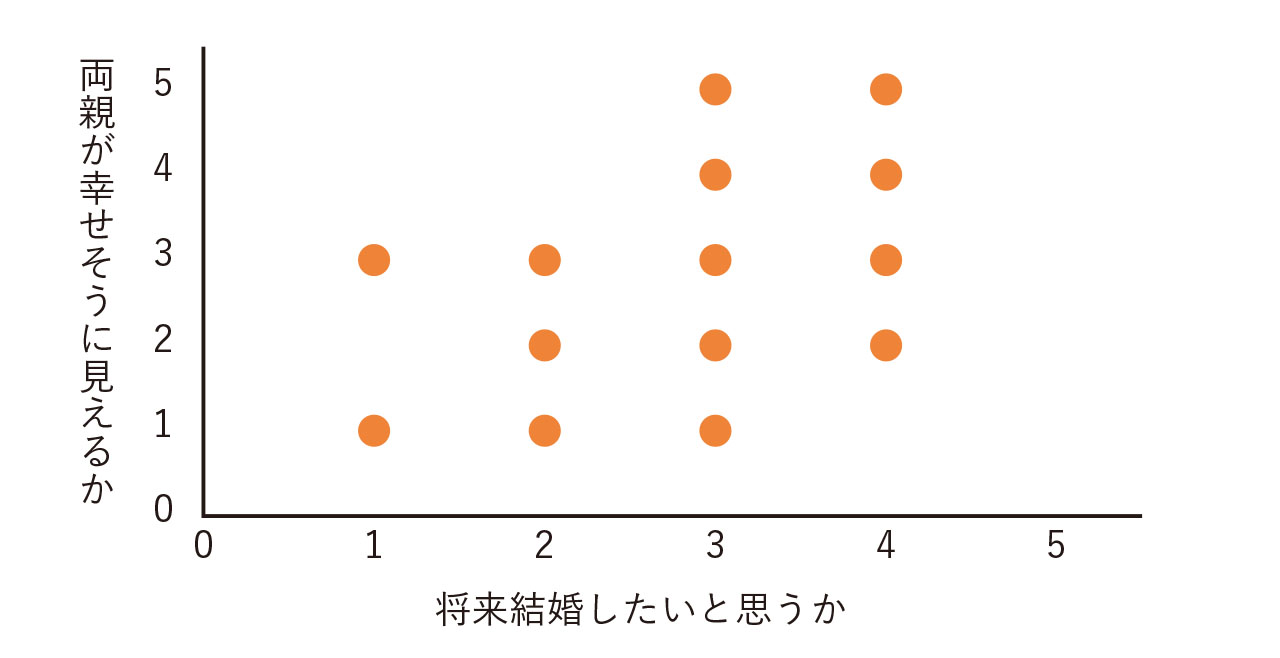
比較は、データの特徴を見る基本的な方法であるとともに、興味深い結果を得る強力な方法です。図1は、大学生を対象に結婚の希望に関する回答を単純に集計したものです。ここから、どのようなことがいえるでしょうか。大学生の多くはあまり強い結婚希望を持っていないと言えるかもしれません。
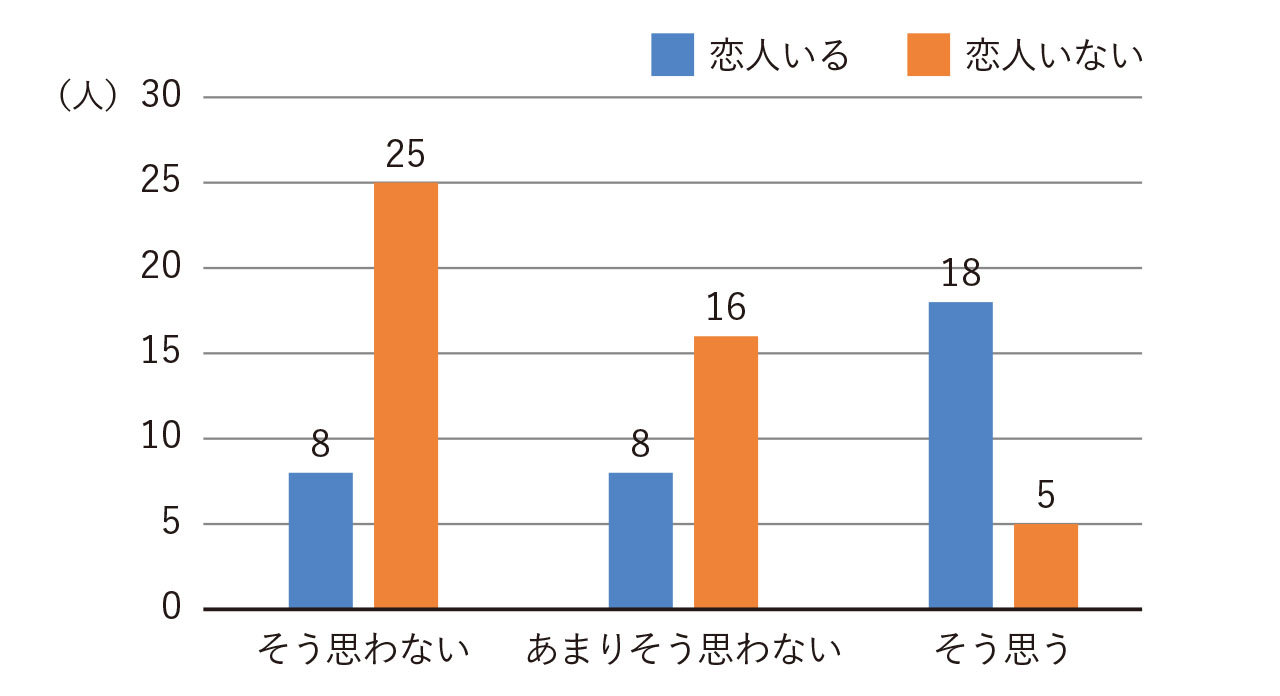
一方、図2を見ると同じことが言えるでしょうか。これらは、同じ質問に対して属性別に集計したものです。図1を見るだけではわからなかったことが言えるようになります。
このように、集めたデータについて属性別に集計することを「クロス集計」と呼びます。さまざまな属性を用いて比較を行うと、興味深い結果を得ることができます。
データの関係を見る
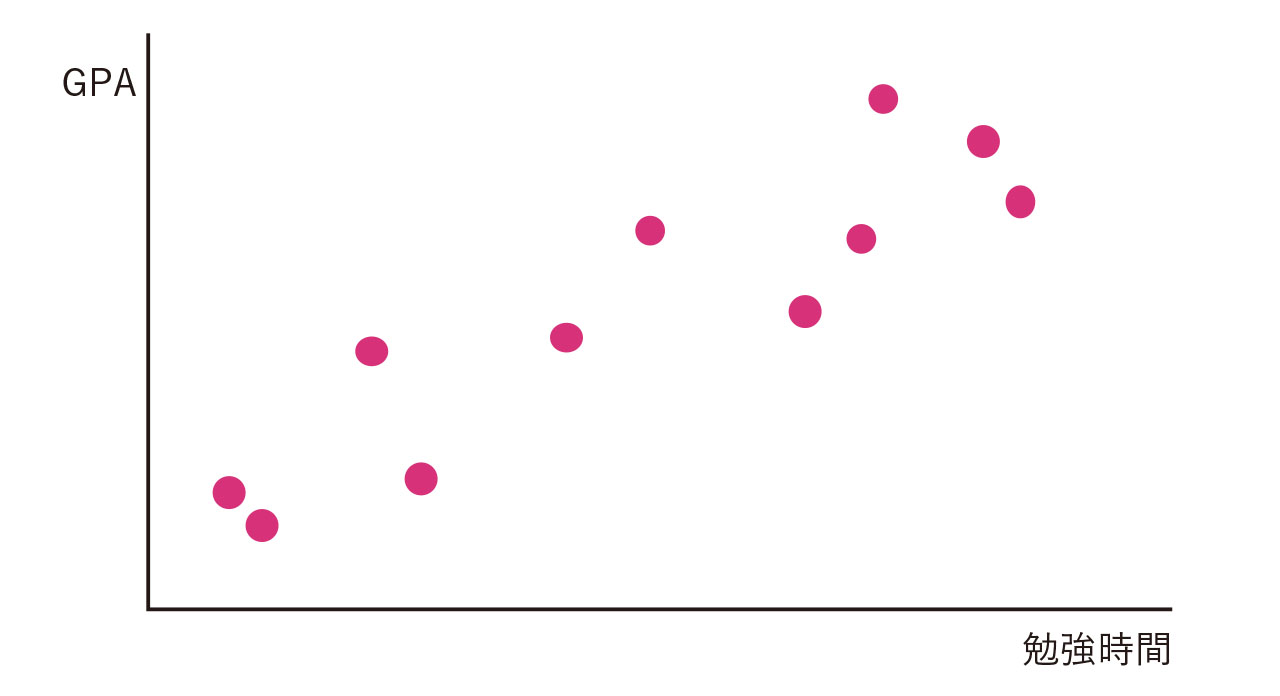
2つのデータの関係を見るとは、相関関係があるかどうかを見ることです。相関関係があるかを見るには、散布図を描いて調べます。たとえば、大学での勉強時間の長さと学期末のGPAの間にはどのような関係があるでしょうか。図3のような関係があるなら、勉強時間が長い人ほど、成績が良いと言えそうです。連続的な値を取る数字は、散布図を描きましょう。
一方、調査で得られるデータには、「全くそう思わない」から「とてもそう思う」のように尺度で尋ねるものもあります。そうしたデータで散布図を描いても、図4のようになり、関係がよくわかりません。この場合は、「順位相関係数」を計算することで関係の有無を確かめることができます。
順位相関係数は-1から1の値をとる係数で、1に近づくほど正の関係が、-1に近づくほど負の関係があり、0に近いほど2つの変数に関係がないことを意味します。
疑似相関に注意する
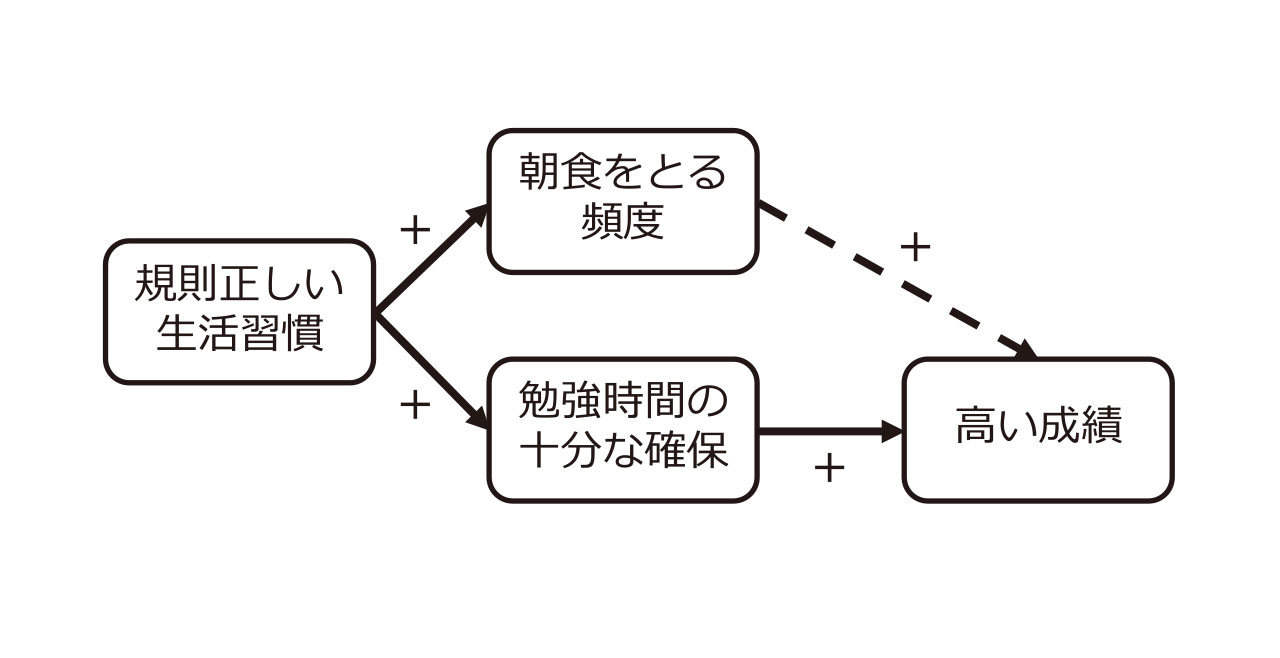
「毎日朝食をとる人ほど成績が良い」と聞いて、あなたは毎日朝食を食べようと思うでしょうか。実際に調査すると、朝食の回数と学校の成績に正の相関関係があるようです。だからといって、ただちに成績を上げるために朝食をとろうと主張してはいけません。
朝食をとる背後には、規則正しい生活習慣があるかもしれません。規則正しい生活習慣は、勉強時間の十分な確保にもつながるため、高い成績の原因は勉強時間かもしれません。朝食の回数と成績は見せかけの相関関係をとらえた可能性があります。
相関関係を見る時は、2つの変数の背後に真の要因が存在するのではないか?という疑問を持って考察しましょう。
発展的な学習のために
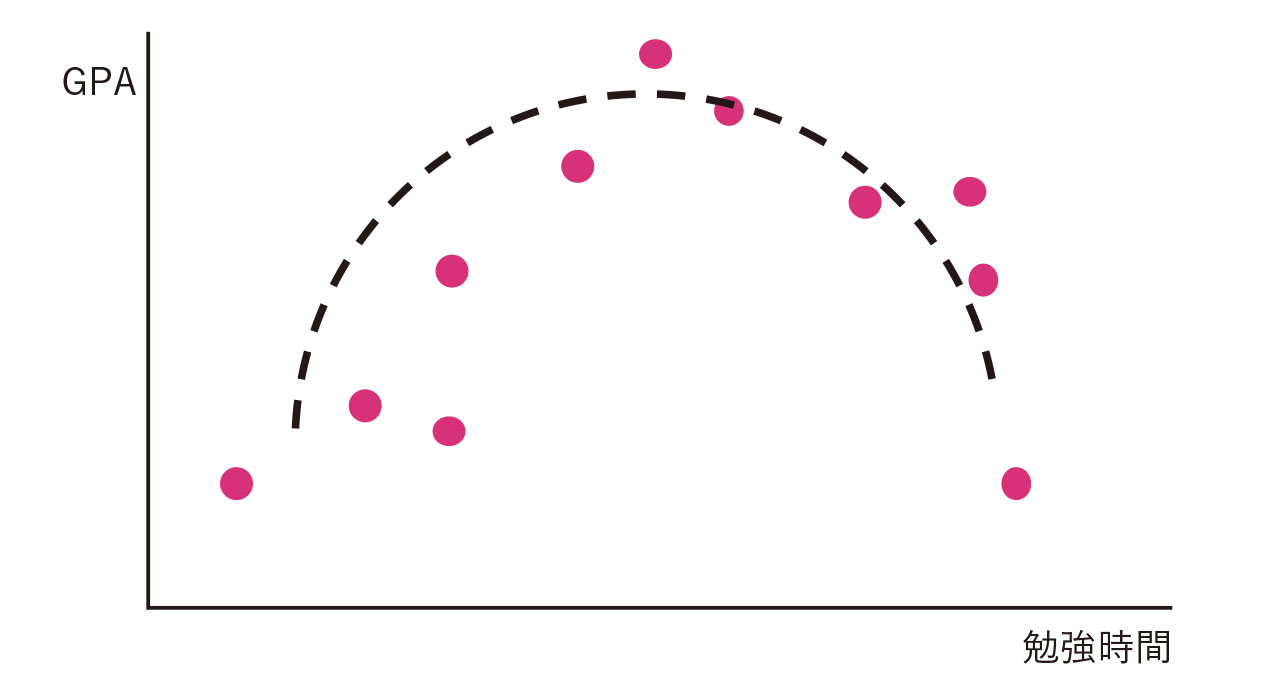
図2で「あまりそう思わない」という回答は、8件と16件という差があります。この差は意味がある差と言えるでしょうか。あるいは、本来は差がないにもかかわらず、たまたま今回の調査で差があるように見えたのでしょうか。これを確かめるには仮説検定が必要です。また、図6のような2次曲線の関係では相関係数が0に近くなり、本来関係があるにもかかわらず見落とす可能性もあります。基礎的な統計学を学ぶことで、より説得力のある議論に発展させることができます。
- 推薦文献
- 石村貞夫・加藤千恵子・劉晨(2009)『やさしく学ぶ統計学 Excelによるアンケート処理』東京図書.
- 発行|
- 名古屋大学教養教育院 & 高等教育研究センター
- 初版|
- 2018.3.20
- 作成|
- 中島 英博